Est-ce vrai, tout ça ?

par Pierre Paquette

Nous vivons dans un monde où les faits semblent de moins en moins importants, 38 % des Québécois affirmant qu’ils croiraient plus une fausse nouvelle rejoignant leurs sentiments qu’une vraie nouvelle allant à l’encontre de leurs croyances. L’Univers qui nous entoure est tellement vaste que cela peut en être déconcertant ; comment croire les affirmations des astronomes ? Il est évident que personne n’est allé mesurer l’Univers sur place…

Le premier jalon dans l’échelle cosmique est la forme et la taille de la Terre. Debout dans un champ, nous avons l’impression que la Terre est plate — et certaines personnes le croient encore ^[1]. De nombreuses preuves à l’appui du contraire existent pourtant, comme le fait qu’il n’est pas la même heure dans tous les pays du monde — les Parisiens se réveillent tandis que les Californiens vont au lit — ou que l’on ne voit pas les mêmes étoiles au nord et au sud de l’équateur terrestre. Mais si vous n’avez jamais voyagé, comment pouvez-vous vous assurer de la véracité des témoignages d’autres gens ?

1) Forme de la Terre

La plupart des sites web indiquant comment prouver la forme de la Terre impliquent de se déplacer loin, ce qui peut ne pas être facile si on ne peut se permettre la dépense financière associée, ou d’attendre de longues périodes de temps pour observer plusieurs éclipses totales de Lune. Mais il suffit de grimper !

Hauteur (m)	Distance à l’horizon (km)
0	0
1	3,6
5	8
100	36
828 (Burj Khalifa)	103
8 848 (mont Everest)	336
11 000 (avions)	375

En effet, comme l’indique la Figure 1 de gauche, si la Terre était plate, nous pourrions voir les choses très lointaines, peu importe notre hauteur. En réalité, la rotondité de la Terre nous empêche de voir les objets lointains, mais si l’on monte à une plus haute altitude, nous verrons un peu plus loin… Pas besoin d’escalader de montagne ; le tableau de droite nous montre jusqu’à quelle distance une personne peut voir selon la hauteur. Si la Terre était plate, la distance à l’horizon serait toujours la même, peu importe l’altitude.

Nous avons donc la preuve que la Terre est ronde, ou du moins courbée, sans vraiment quitter notre domicile… Mais qu’en est-il de sa taille ? La Terre mesure-t-elle quelques kilomètres de diamètre ? quelques centaines de kilomètres ?

2) Taille de la Terre

À strictement parler, il est possible de calculer la taille de la Terre sans se déplacer, en connaissant la distance de l’horizon — on peut y envoyer une autre personne ou noter un objet qui s’y situe. La distance à l’horizon (lien en anglais ; la version française est moins complète) est égale à d² = h(D + h), où d est la distance à l’horizon, h est la hauteur au-dessus du niveau de la mer, et D est le diamètre de la Terre. Si une personne ou un objet est visible à 8 km tandis que l’on est à 5 m au-dessus du niveau de la mer, alors 8 000² = 5 * (D + 5), donc 64 000 000 = 5 * (D + 5), donc 12 800 000 = (D + 5), donc D = 12 799 995 m ; la Terre mesure donc environ 12 800 km de diamètre — c’est en fait 12 756 km, soit moins de 0,3 % d’erreur. (Idéalement, il faut aussi tenir compte de la réfraction atmosphérique, qui ajoute environ 8 % à la distance de l’horizon.)

3) Distance de la Lune

Pour trouver la distance à la Lune sans nous déplacer, nous devons attendre une éclipse totale de Lune et faire quelques suppositions : d’abord, que l’orbite de la Lune est circulaire ; ensuite, que la Lune est assez proche et le Soleil assez loin pour que l’ombre de la Terre à la distance de la Lune ait environ le même diamètre que notre planète.

Pour parcourir son orbite, d’un rayon R et donc de circonférence 2 π R, la Lune requiert un temps T. De même, elle traverse diamétralement l’ombre de la Terre (de rayon r donc de diamètre 2r) en un temps t. Le rapport des deux tailles est donc proportionnel au rapport des deux temps, et on a 2 π R ÷ 2 r = T ÷ t. Par l’observation, on détermine facilement que T vaut environ 27½ jours (entre deux passages successifs de la Lune vis-à-vis une même étoile) et que t vaut environ 3½ heures. À la section 2, on a vu que r = 6 400 km, donc 2πR ÷ 12 800 = 27½ ÷ (3½ ÷ 24), ce qui se simplifie à R = 384 154,56 km. Ceci est très près de la réalité ; la distance à la Lune varie de 356 400 à 406 700 km…

4) Diamètre de la Lune

Maintenant que nous connaissons le diamètre de la Terre et la distance de la Lune en kilomètres, la trigonométrie de base nous donnera le diamètre réel de la Lune. À l’œil nu, il est possible d’obtenir une précision suffisante dans la mesure du diamètre angulaire de notre satellite : environ 31′ (cela varie selon sa distance à la Terre). En suivant le graphique ci-contre, il s’agit de mesurer l’angle ∠AOA′, qui correspond au diamètre angulaire de la Lune telle que vue depuis la surface de la Terre. L’angle ∠AOB est égal à la moitié de l’angle ∠AOA′. Par trigonométrie, on a r ÷ (d − R) = tan ∠AOB.

Puisque l’angle ∠AOA′ est mesuré à 31′, on a ∠AOB = 15,5′, soit 0,258333…°, donc tan ∠AOB = 0,004509. On sait que d = 384 154,56 km, tel que calculé précédemment, et que R = 12 800 km, donc d − R = 371 354,56 km. Ainsi, r = 0,004509 · 371 354,56, donc r = 1 674,36 km, ce qui donne un diamètre de 3 348,7 km pour la Lune (son diamètre réel est de 3 476,2 km ; notre erreur est donc d’environ 3,7 %, attribuable aux faits que la distance de la Lune est variable et que nous ayons mené notre observation à l’œil nu, offrant donc une précision faible).

5) Distance du Soleil

Lorsque la face visible de la Lune est éclairée exactement à moitié (premier ou dernier quartier de Lune), cela signifie que l’angle entre le Soleil et nous tel que mesuré depuis la Lune est égal à 90°. En mesurant l’angle θ entre la Lune et le Soleil à ce moment-là, on peut déduire la distance du Soleil, tel que le montre le schéma ci-contre.

Toujours par trigonométrie, on a L ÷ S = cos θ, donc en inversant le tout, S ÷ L = 1 ÷ cos θ. Le problème consiste à mesurer θ précisément, ce qui est difficile à cause de l’éclat du Soleil ; l’astronome grec Aristarque de Samos (v. 250 AÈC) est arrivé à 87°, mais nous mesurons 89° 51′ — il est possible d’atteindre une telle précision en utilisant un filtre solaire, qui n’existait pas à l’époque d’Aristarque.

Le membre de droite de l’équation (1 ÷ cos θ, soit 1 ÷ cos 89° 51′ ou encore 1 ÷ 0,00261799) est égal à environ 381,972, ce qui signifie que le Soleil est environ 382 fois plus distant de nous que la Lune ne l’est ; sa distance est donc de 384 154,56 km × 381,972 = 146 736 400,744 km (c’est en fait quelque 149 600 000 km, mais encore une fois, nos mesures sont approximatives).

6) Les planètes

Les Anciens ont remarqué que sept astres se déplacent dans le ciel au fil du temps, à divers rythmes : en ancien grec, ce sont les πλάνητες ἀστέρες « planètes astéres », soit en français « astres errants » ; le premier terme a été francisé et est devenu notre mot « planète ». Ces astres errants étaient pour les civilisations anciennes des divinités (voir tableau ci-dessous) ; nous utilisons les noms latins francisés — Mercure, Vénus, Mars, Jupiter, et Saturne — pour cinq d’entre elles, les deux autres étant le Soleil et la Lune. Le mouvement des sept astres errants, comme celui de la sphère céleste, était considéré comme circulaire et centré sur la Terre, que les Anciens croyaient à tort être le centre de l’Univers ^[2].

Dans l’ordre des distances à la Terre, on retrouvait la Lune, Mercure, et Vénus, puis le Soleil, au-delà duquel se trouvaient ensuite Mars, Jupiter, et Saturne. Cet ordre a été établi selon le temps que prenait chaque astre pour revenir à un même point par rapport aux étoiles (ce que l’on appelle sa « période synodique »).

Noms des planètes classiques dans diverses cultures (Cliquer pour afficher ▶)

sumérien, akkadien1	akkadien, babylonien1	égyptien	ancien grec	latin	sanskrit	hébreu	arabe	chinois (mandarin)	japonais2	vietnamien2
𒀭𒌓 dUD = Utu	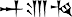dŠa‑maš (seigneur du ciel et de la terre)	jtn = Aten	Ἥλιος Helios	Sol	सूर्य Sūrya	שֶׁמֶשׁ šɛmɛš ou חמה ḥmh Ḥammah, le chaud (dans le Talmud)	الشمس al‑Shshams	太阳 Tàiyáng, le grand Yang	太陽 Taiyō	mặt trời
dŠEŠ.KI, dNANNA	dEN.ZU (seigneur de la sagesse ; mais prononcé Sîn)	Jˁḥ = Iah	Σελήνη Selenê	Luna	चन्द्र Candra	ירח rḥ ou לבנה lḇnh Levanah, la blanche	القمر al‑Qamar	月亮 Yuèliàng, la brillante mensuelle	月 Tsuki	Mặt trăng
𒂗𒆠 dEN.KI(G), plus tard appelé Ea	MULNa‑bu‑u2	ḏḥwty = Thoth, peut-être Sabgu	Ἑρμῆς Hermes	Mercurius	बुध Budha (ou सौम्य Saumya)	כּוככ חמּה‎ kokhav khamma ou נבו nḇw Nevo, la planète	عطارد ‘Otared	水星 Shuǐxīng, l’étoile d’eau	水銀 Suigin	Sao Thủy Tinh
𒀭 Ištar, Inanna	dIš‑tar	Sekhmet	Αφροδίτη Aphroditê3	Venus	शुक्र Śukra	כוכבת ḵwḵḇṯ Kokhevet, נוגה nwḡh Nogah, ou כוכב נוגה ḵwḵḇ nwḡh Kokhav‑Nogah, la planète brillante	الزهرة al‑Zuhrah	金星 Jīnxīng, l’étoile de métal	金星 Kinboshi	Sao Kim
𒀭𒄊𒀕𒃲 dGÌR‑UNUG‑GAL (lu « Nergal »)	MULSal‑bat‑â‑nu	ḥr.w = Horus, plus tard Ḥr Dšr, « Horus le Rouge »	Ἄρης Ares	Mars	मङ्गल Maṅgala	מאדים mḏm Ma'adim, la rouge	المريخ al‑Mirrekh	火星 Huǒxīng, l’étoile de feu	火星 Kasei	Hỏa Tinh
𒂗𒇸 dEN.LIL, seigneur de la tempête	Marduk, ou MUL2 BABBAR (« étoile blanche » ; notre image)	imn = Amon, aussi Her‑wepes‑tawy	Ζεύς Zeus	Iuppiter	बृहस्पति Bṛhaspati	צדק ṣḏq Tzedeq, justice	المشتري al‑Mushtari	木星 Mùxīng, l’étoile de bois	木星 Mokusei	Sao Mộc
Ninurta	dNin‑urta	Heru	Κρόνος Kronos	Saturnus	शनि Śani	שַׁבְתַאִי šaḇṯaʾī Shabbatai, la calme	زحل Zuhal	土星 Tǔxīng, l’étoile de terre	土星 Dosei	Sao Thổ
En sumérien, akkadien, et babylonien, on trouve souvent plusieurs noms pour le même astre ; par exemple, Kasak et Veede (2001:22) indiquent que Jupiter avait au moins douze noms différents selon le mois. Un de ces noms est Nibiru, pour le mois de Tišrîti, prouvant que l’hypothèse d’une autre planète ainsi nommée est fausse — surtout que le terme pouvait aussi être utilisé pour désigner l’Étoile polaire (α UMi), Canopus (α car), la constellation de Persée, ou même un météore ! Dans ces langues, d (abréviation de DINGIR) est le symbole pour une divinité (𒀭 en sumérien ; simplifié en en akkadien), tandis que MUL est le symbole pour une étoile ou un astre (𒀯 ; devenu en akkadien — toujours trois DINGIR ensemble). Ces symboles n’étaient jamais prononcés. (Un important catalogue babylonien d’étoiles est le MUL.APIN, 𒀯𒀳 ; les Pléiades sont MUL.MUL, « l’étoile d’étoiles », 𒀯𒀯) Les noms japonais et vietnamiens ont la même signification que les noms chinois (sauf pour le Soleil et la Lune). Le mot vietnamien Sao signifie « étoile ». Vénus était aussi appelée Ἓσπερος, Hesperos, lorsqu’elle était observée le soir, et Φωσφόρος, Phōsphoros, le matin, jusqu’à ce que Pythagore (?) réalise qu’il s’agissait d’un seul et même astre.
Sources : LITTLE, Robert. Names of the Planets, 2008 Quora. What is the oldest name for earth? Arabic Way. Planets 1930–2006 KASAK, Enn, et Raul VEEDE. « Understanding Planets in Ancient Mesopotamia. » Folklore Vol. 16, p. 7–33, novembre 2001. ZUCKER, Shay. « Hebrew names of the planets. » The Role of Astronomy in Society and Culture, Proceedings of the International Astronomical Union, IAU Symposium Vol. 260, p. 301–305, juin 2011.

Les Anciens ont aussi remarqué que Mercure et Vénus ne s’éloignent jamais beaucoup du Soleil : une vingtaine de degrés tout au plus pour Mercure, tandis que Vénus s’aventure à une quarantaine de degrés de l’astre du jour.

L’animation ci-contre représente le mouvement de Mercure ou de Vénus dans les modèles de Ptolémée ou d’Aristote. Si leur orbite était un cercle simple parcouru à vitesse uniforme — précepte de base de tout mouvement céleste selon eux —, elles resteraient pas à faible distance angulaire du Soleil, mais se retrouveraient plutôt n’importe où le long de l’écliptique. Un épicycle (orbite secondaire parcourant l’orbite principale) doit donc être ajouté, leur permettant de toujours être à l’intérieur d’une certaine distance angulaire du Soleil, telles que vues de la Terre. Le système est ici simplifié, avec la Terre au centre, mais dans ses dernières ramifications, le centre de l’orbite principale était un point imaginaire décalé de la Terre, avec entre les deux un autre point imaginaire du point de vue duquel le mouvement était uniforme — un vrai casse-tête, avec pas moins de soixante-dix cercles dans certaines versions !

Mais revenons plutôt à l’animation. Cliquez sur le rectangle vert pour démarrer l’animation ; un rectangle rouge apparaitra alors, sur lequel vous pourrez cliquer pour arrêter l’animation. Le cercle jaune représente le Soleil ; le cercle bleu est la Terre, au centre. Le cercle gris et blanc est Mercure ou Vénus — les planètes Mars, Jupiter, et Saturne orbitent au-delà du Soleil dans le modèle de Ptolémée, et ne sont pas représentées ici, ni la Lune, qui orbite plus près de la Terre que ne le font Mercure et Vénus.

La fenêtre en bas à droite indique la phase de la planète observée (amplifiée pour clarté) ainsi que la position de celle-ci par rapport au Soleil — le diagramme n’est pas à l’échelle. Pour simplifier, nous avons fait abstraction de la position de la planète en hauteur (latitude géocentrique). Vous remarquerez que la planète ne montre jamais plus qu’un mince croissant. Toutefois, à l’œil nu, la planète est assez loin qu’elle n’apparait que sous la forme d’une étoile, sans dimension apparente, alors il a fallu attendre l’invention d’instruments optiques grossissants pour progresser sur cette question.

Mercure et Vénus

Selon le modèle de Ptolémée tel qu’illustré dans l’animation ci-dessus, si Mercure et Vénus orbitaient au-delà du Soleil, tout en restant à quelques dizaines de degrés de lui, elles seraient toujours presque entièrement éclairées ; si à l’inverse elles orbitaient entre le Soleil et nous, elles se présenteraient à nous toujours sous l’aspect d’un croissant, et jamais éclairées plus qu’à la moitié.

Or, lorsque Galilée pointe sa lunette d’approche sur Vénus, du 1^er octobre au 30 décembre 1610, il observe que celle-ci présente des phases semblables à celles de la Lune (L’Essayeur, 1623, p. 217 ; voir image ci-contre). Comme nous venons de le voir, une telle chose serait impossible selon le modèle de Ptolémée. Toutefois, quelques dizaines d’années auparavant (1543), Nicolas Copernic a proposé un nouveau système, dans lequel ce n’est plus la Terre, mais bien le Soleil qui est au centre du système solaire. Les nouvelles observations de Galilée sont en parfait accord avec le modèle de Copernic, au grand dam de l’Église et de l’Inquisition, qui accusent Galilée d’hérésie — mais tout cela est une autre histoire !

Dans le modèle de Ptolémée, Mercure et Vénus pouvaient être à n’importe quelle distance du Soleil sans qu’il soit vraiment possible de calculer cette distance, mais dans le modèle de Copernic, la taille de leur orbite telle que vue de la Terre nous permet de déterminer leur distance absolue, du moment que l’on connait la distance du Soleil. Ainsi, en mesurant la largeur angulaire de l’orbite de Mercure ou de Vénus, on peut calculer leur distance, comme dans le schéma ci-contre. Nous connaissons D, la distance Terre–Soleil (voir ci-dessus ; nous prenons la valeur de 146 737 165 km obtenue avec une mesure de l’écart angulaire Lune–Soleil de 89° 51′ plutôt que la valeur réelle, question de toujours demeurer au plus simple). En mesurant les angles θ_M pour Mercure et θ_V pour Vénus, nous pourrons trouver d_M, la distance Soleil–Mercure, de même que d_V, la distance Soleil–Vénus. Ces deux valeurs seront calculées par les formules d_M = D sin θ_M et d_V = D sin θ_V.

L’observation de Mercure, faite au moment de sa plus grande élongation ouest le 19 janvier 2017, nous donne θ_M = 24,1° ; pour Vénus, nous l’avons mesurée à sa plus grande élongation est le 12 janvier 2017, et obtenu θ_V = 47,1°. Nous obtenons donc :

d_M = 146 737 165 · sin 24,1° = 59 917 254 km pour Mercure, et
d_V = 146 737 165 · sin 47,1° = 107 491 268 km pour Vénus

Ces valeurs sont assez rapprochées de la réalité (57 909 050 km pour Mercure, variant de 46 001 200 km au périhélie à 69 816 900 km à l’aphélie ; et 108 208 000 km, variant de 107 477 000 km au périhélie à 108 939 000 km à l’aphélie pour Vénus), surtout si l’on considère que nous n’avons utilisé qu’une valeur approximative pour la distance Terre–Soleil…

Les planètes extérieures : Mars, Jupiter, et Saturne

Le problème du calcul de la distance des planètes extérieures (Mars, Jupiter, et Saturne) au Soleil est plus complexe, car nous nous trouvons à l’intérieur de leur orbite. Nous avons donc besoin de connaitre leur période sidérale de révolution, c’est-à-dire le temps qu’elles prennent pour faire un tour complet autour du Soleil par rapport aux étoiles (à la même longitude écliptique). Prenons par exemple l’observation de Jupiter le 1^er avril 2017, à 00 h 00 TU : sa longitude écliptique est de 199° 08′, ce qui la place juste à côté de θ Vir. À strictement parler, il faudrait attendre le prochain 1^er avril à 00 h 00 où la longitude écliptique de Jupiter est de 199° 08′ (avec quelque marge d’erreur permissible), puis diviser par le nombre d’années écoulées ; cela risquerait d’être long !

Heureusement, Copernic a découvert une relation très simple entre les orbites d’une planète extérieure et de la Terre, en lien avec le schéma ci-contre (cliquer sur « D’où vient cette formule » pour afficher) : 1 ÷ S = 1 ÷ T − 1 ÷ P (la relation est inversée pour les planètes intérieures Mercure et Vénus à 1 ÷ S = 1 ÷ P − 1 ÷ T). Ici, l’angle S est plus facile à évaluer, car il correspond à la période synodique de révolution de la planète, c’est-à-dire le temps qu’elle prend pour être vis-à-vis d’une même étoile (à la même longitude écliptique) par rapport à la Terre. Dans cette formule, T est le temps requis à la Terre pour compléter son orbite autour du Soleil par rapport aux étoiles (année sidérale ; 365,25636 jours).

Planète	Période synodique observée	Période sidérale calculée	Vraie valeur
Mars	778,0 j	688,489 j = 1,885 a	686,971 j = 1,8808 a
Jupiter	398,9 j	4 330,707 j = 11,857 a	4 332,59 j = 11,8618 a
Saturne	378,1 j	10 752,671 j = 29,439 a	10 759,22 j = 29,4571 a
Uranus	369,7 j	30 388,437 j = 83,198 a	30 688,5 j = 84,0205 a
Neptune	367,6 j	57 290,470 j = 156,850 a	60 182 j = 164,8 a
Les différences s’expliquent entre autres par le fait que les vraies valeurs proviennent de Wikipédia, qui les donne en années juliennes de 365,25 j plutôt qu’en années sidérales de 365,25636 j. De plus, chaque orbite planétaire est sujette à des perturbations par les autres planètes, alors la période de révolution n’est qu’une moyenne sur plusieurs années, la période instantanée étant différente (voir par exemple l’Observer’s Handbook de la Société Royale d’astronomie du Canada).

En utilisant cette formule et en mesurant la période synodique de chaque planète (temps écoulé entre deux passages à la même longitude écliptique telle que vue de la Terre), nous pouvons calculer sa période de révolution sidérale. Nos résultats paraissent dans le tableau ci-contre, qui en plus des planètes classiques de l’Antiquité inclut aussi les planètes Uranus et Neptune, découvertes en 1781 et 1846, respectivement.

Une fois que nous avons trouvé la véritable période de révolution de la planète autour du Soleil, nous pourrons calculer sa distance, en mesurant l’intervalle de temps entre son opposition et sa quadrature. Disons que t est cet intervalle. Pendant celui-ci, la Terre aura parcouru autour du Soleil un angle α = t × (360° ÷ T), où T est l’année sidérale de la Terre (voir l’encadré « D’où vient cette formule ? » ci-contre). De même, pendant ce temps, la planète aura parcouru un angle β = t × (360° ÷ P), où P est l’année sidérale de la planète, que l’on vient de calculer.

Comme nous le montre le graphique ci-contre, la différence entre ces deux angles (α − β) est égale à l’angle Terre–Soleil–planète lors de la quadrature. La trigonométrie de base nous dit alors que la distance entre la planète et le Soleil est donnée par d = 1 ÷ cos (α − β).

Prenons l’exemple de Mars lors de son apparition de 2016 : l’opposition a eu lieu le 22 mai et la quadrature Est le 13 septembre. La différence de temps entre l’opposition et la quadrature Est est de 114 jours ; pendant ce temps, la Terre a parcouru 114 × (360° ÷ 365,25636) degrés sur son orbite, soit 112,36°. Mars, quant à elle, a parcouru 114 × (360° ÷ 688,489) degrés, soit 59,6° (la valeur de la période sidérale est celle que nous avons estimée ci-dessus).

La différence entre ces angles (α − β) est de 52,76° ; donc 1 ÷ cos (α − β) = 1,652469, ce qui représente la distance Soleil–Mars par rapport à la distance Soleil–Terre — pas trop mal comme calcul approximatif, puisque la réalité est de 1,523679 (erreur de 8 %), mais cette distance varie de 1,666 à 1,3814 selon où Mars se trouve sur son orbite elliptique et excentrique par rapport au Soleil. Comme sources d’erreur, mentionnons les faits que nous supposons des orbites circulaires tandis qu’elles sont elliptiques, que nous avons pris une valeur calculée approximativement pour la période sidérale de Mars, et que les dates et angles mentionnés ne sont qu’approximatifs. En multipliant 1,523679 par 146 737 165 km obtenu plus tôt, nous obtenons 223 580 337 km comme distance Soleil–Mars.

7) Les étoiles

Les étoiles sont si loin qu’il est difficile de mesurer leur distance. La méthode la plus évidente est celle de la parallaxe, mais les angles à mesurer sont si faibles qu’ils ne furent détectés qu’en 1838 ! En fait, leur non détection avait souvent utilisée comme « preuve » que la Terre est au centre de l’Univers…

Le principe est pourtant simple : mesurer la différence de position de l’étoile étudiée entre deux dates séparées de six mois, de sorte que la Terre soit de part et d’autre du Soleil. Par trigonométrie, on trouve que la distance de l’étoile est égale à la distance Terre–Soleil divisée par la tangente de l’angle mesuré. Toutefois, ledit angle est toujours faible, comme nous l’avons vu au dernier paragraphe : même l’étoile la plus rapprochée n’a une parallaxe que de 0,77″ — cela est équivalent à un grain de sable de 0,5 mm vu à une distance de 134 m !

Qu’en est-il des étoiles ? Cet angle de 0,77″, combiné à la distance Terre–Soleil que nous avons mesurée (146 737 165 km), nous donne une distance pour l’étoile (en l’occurrence Proxima du Centaure) de 39 307 419 360 822 km. Proxima est l’étoile la plus proche de nous (d’où son nom !), ce qui signifie que les autres étoiles sont plus loin encore — et habituellement, beaucoup plus loin…

Nous avons donc besoin d’une unité de mesure qui soit plus pratique que le kilomètre — même pour les planètes, nous parlions déjà en centaines de millions ou en milliards de kilomètres ; les astronomes utilisent habituellement l’unité astronomique, initialement définie comme étant la distance moyenne Terre–Soleil (mais aujourd’hui raffinée à exactement 149 597 870,7 km), pour mesurer les distances planétaires. Pour les distances stellaires, on a recours à l’année-lumière (une unité de distance, et non de temps !), définie comme étant la distance parcourue par la lumière dans le vide en une année julienne (365,25 jours) à la vitesse c = 299 792 458 m/s. Cela donne 9 460 730 472 580 800 m.

Si l’on revient à Proxima du Centaure, cela donne une distance de 4,15 années-lumière (valeur réelle : 4,246 ±0,006 a.‑l. ; erreur d’environ 2,2 %). Sirius (α CMa), l’étoile la plus brillante du ciel, a une parallaxe de 0,38″, donc une distance (réelle) de 8,60 ±0,04 a.‑l. ; Procyon (α CMi), 0,28″ ou 11,46 a.‑l. ; Altaïr (α Aql), 0,19″ ou 16,73 a.‑l. ; aucune autre étoile brillante ayant un nom propre n’a de parallaxe supérieure à 0,15″.

Nous arrêterons ici notre série de démonstrations des mesures astronomiques, puisque celles-ci deviennent de plus en plus difficiles à faire (voir l’Annexe ci-dessous pour les instruments qui permettent de faire de telles mesures), mais quelques mots avant de terminer… L’étude des spectres stellaires, aujourd’hui accessibles à certains amateurs bien équipés, permet d’identifier leur composition, initialement par comparaison avec les spectres de substances terrestres. Éventuellement, la classification des étoiles en groupes d’étoiles au spectre semblable permet de déduire que ces étoiles ont toutes à peu près le même éclat intrinsèque, ce qui signifie qu’une étoile quatre fois moins brillante qu’une autre de même type spectral sera deux fois plus loin que la première (puisque la luminosité diminue avec le carré des distances). On put éventuellement appliquer nos connaissances aux galaxies, suite à la découverte d’étoiles variables d’un certain type dans certaines galaxies, et cela nous donna l’échelle des distances cosmiques, base de l’astrophysique moderne.

---

Annexe : Instruments

Nous avons vu que la plupart de nos calculs dépendaient de mesures d’angles ; parfois de grands angles, parfois des angles plus petits — mais toujours mesurés précisément. Quels instruments nos ancêtres ont-ils utilisés pour faire ces mesures et en arriver aux connaissances que nous avons aujourd’hui ? Newton dit un jour que « si j’ai vu si loin, c’est parce que j’ai grimpé sur les épaules de géants », en parlant des scientifiques qui sont venus avant lui, mais ces géants avaient de bonnes échasses avec tous ces instruments !

Le bâton de Jacob est essentiellement une croix de bois dans laquelle la pièce perpendiculaire (le marteau) coulisse sur la pièce principale (la flèche). Si on mesure par exemple l’angle entre deux objets célestes, on fait coulisser le marteau sur la flèche jusqu’à ce que les deux objets soient placés à chaque extrémité du marteau.

L’animation interactive ci-contre vous permet d’approcher ou d’éloigner le marteau de l’œil le long de la flèche d’un bâton de Jacob virtuel. Au haut de la figure se trouvent les boutons pour approcher (⊕) ou éloigner (⊖) le marteau ; au bas de la figure se trouve l’angle mesuré.

Cet angle est donné par la formule α = 2 atan((a ÷ 2) ÷ d), où d est la distance entre l’œil et le marteau, et a est la longueur du marteau, exprimés dans la même unité.

Certains modèles de bâtons de Jacob avaient plus d’un marteau, comme sur notre photo de gauche ; sur d’autres, c’est la flèche elle-même qui était extensible, comme sur notre photo de droite.

L’origine du bâton de Jacob est débattue ; Rabbi Levi ben Gershom ^[3] est le premier à le décrire, mais W.E. May, dans son Histoire de la navigation marine, indique que son origine pourrait remonter aux Chaldéens vers 400 AÈC, et le scientifique chinois Shěn Kuò ^[4] décrit un instrument semblable dans ses Discussions de pinceau depuis un petit ruisseau de rêve ^[5].

Le quadrant est un quart de cercle (d’où son nom) dont le pourtour est gradué en degrés — un peu comme un rapporteur d’angle moderne. Sur le côté du quadrant pend un fil à plomb ; en pointant l’objet étudié avec un côté du quadrant, le fil tombe vis-à-vis l’angle correspondant à sa hauteur dans le ciel. Il en existe divers modèles, parfois avec certains raffinements, mais le principe et l’utilité demeurent essentiellement les mêmes.

Le plus important ajout au quadrant est le vernier, une échelle augmentant la précision, puis un jeu de miroirs permettant de doubler celle-ci, et éventuellement, une petite lunette d’approche. À partir du moment de l’ajout de miroirs, il devient inutile de conserver les 90° de l’objet, et on peut le réduire à 60°, permettant de mesurer des angles jusqu’au double (grâce aux miroirs), donc 120°. Il ne reste donc qu’un sixième de cercle, d’où le nom de sextant.

La lumière de l’astre mesuré est d’abord réfléchie par le miroir d’index (A), puis par le miroir d’horizon (B), avant d’entrer dans la lunette (C). Le sextant servant beaucoup en mer pour déterminer la latitude, en partant de la mesure de la hauteur du Soleil (ou d’un autre astre) au-dessus de l’horizon, on ajoute des filtres (D et E) au sextant pour diminuer l’éclat du Soleil quand c’est celui-ci que l’on mesure. La mesure de l’angle est indiquée en F, et précisée à la vis micrométrique (G).

Le fait que le miroir d’index soit mobile par rapport au miroir d’horizon est ce qui permet de doubler l’angle mesuré, et donc d’obtenir une mesure précise.

Notre simulation de sextant, ci-contre, vous permet de voir le fonctionnement de l’appareil. Appuyez sur ⊕ ou sur ⊖ pour voir la flèche pivoter selon l’angle de vue (l’animation fonctionne de 0° à 130°). La forme noire est la lunette ; la ligne tiretée orange est la ligne de visée de l’objet observé.

Les meilleurs sextants permettent une précision d’environ 0,2′ = 12″ (à comparer à une précision d’environ 1′ = 60″ à l’œil nu) ; puisque 1′ correspond à un mille nautique, 12″ représente environ 0,1 mille nautique, soit environ 200 m.

L’ancêtre de tous ces instruments est toutefois l’astrolabe (de l’ancien grec ἄστρον, ástron, « étoile » ; et λαμβάνω, lambánō, « je prends »), qui pourrait avoir été inventé vers 200 avant l’ère commune, mais dont le plus ancien spécimen retrouvé date du huitième siècle de l’ère commune. On doit distinguer l’astrolabe marin (image ci-contre) de l’astrolabe astronomique ; le premier est simplement un cercle gradué muni d’une règle de visée, l’alidade (de l'arabe العضادة, al-idhâdah, « réglette »), tandis que l’astrolabe astronomique (ou planisphérique) est plus complexe — voir ci-dessous.

Comme le schéma l’indique, l’astrolabe marin est soutenu par le haut (on le laisse souvent pendre d’un mat), et la règle est ajustée jusqu’à ce que l’objet observé apparaisse dans les pinnules, des « petite[s] plaque[s] de métal percée[s] et disposée[s] à chaque extrémité d’une alidade pour permettre la visée » (selon Wikipédia). Évidemment, quand on vise le Soleil, on ne le regarde pas directement, mais on laisse plutôt l’ombre de la première pinnule tomber à l’endroit propice sur la seconde pinnule.

La précision de l’astrolabe marin dépend de sa taille ; en effet, plus l’instrument est grand, plus fines ses graduations peuvent être. Toutefois, passé un certain format, il devient difficile à tenir ou à manipuler, et un compromis doit être fait.

Les astrolabes marins sont en général évidés (portions blanches dans l’image) pour les rendre plus légers et moins sujets au vent. Leur partie inférieure est parfois plus pleine, question d’aider la gravité à garder l’instrument pendu bien verticalement.

L’astrolabe astronomique ou planisphérique comporte deux faces, chacune munie d’une alidade (ou souvent une simple règle sur la face avant et une alidade au verso). Il n’est pas évidé ; sur sa face avant se trouvent des courbes représentant la hauteur dans le ciel (ou altitude) — ce sont les almicantarats ^[6] — de même que d’autres représentant la direction le long de l’horizon, les azimuts ^[7].

Au dos de l’astrolabe, on trouve un calendrier excentrique ainsi qu’un tracé de l’écliptique, centré. La correspondance de la date avec la position sur l’écliptique, mesurée avec l’alidade, permet de trouver la position du Soleil sur l’araignée, qui est la partie mobile à l’avant (portion dorée sur notre image). Placer cette position en accord avec la hauteur observée du Soleil permet de déterminer l’heure, mais l’astrolabe a de nombreux autres usages, puisque les petites pointes de l’araignée représentent les étoiles, et qu’il y a habituellement d’autres inscriptions ou gravures au dos, comme un carré de hauteur (permettant de connaitre la hauteur d’objets terrestres lointains) ou un graphique des sinus et cosinus.

Selon Janus ^[8], « au dixième siècle, [ʿAbd al‑Rahmân al‑Sûfî ^[9]] a écrit un traité détaillé sur l’astrolabe consistant de 386 chapitres dans lesquels il a décrit 1000 utilisations pour l’astrolabe. [L’astrolabe pouvait servir à] indiquer l’heure pendant le jour ou la nuit, trouver l’heure du lever et du coucher du Soleil et, donc, la durée du jour, à localiser les objets célestes dans le ciel, comme une référence pratique pour les positions célestes et, puisque l’astrologie était un élément profondément enraciné dans les cultures qui utilisaient les astrolabes, pour déterminer les aspects des horoscopes. Les temps des prières islamiques sont déterminés par l’astronomie, et l’astrolabe [peut] être utilisé pour déterminer les temps requis. »

---

Notes

1)   Au début février 2019, une conseillère municipale de la ville de Gatineau a indiqué sur sa page Facebook considérer que la Terre est plate, poussant même jusqu’à demander « Qui a décidé que la Terre est ronde ? »

2)   De placer la Terre au centre de l’Univers était en ligne avec la philosophie aristotélicienne : les Humains sont indignes des sphères cristallines que l’on croit former le cosmos. Il y a notre « bas monde », et il y a le Domaine des Dieux. Pis encore que la Terre est l’Enfer, que l’on considère être au centre de la Terre. À noter que personne à cette époque ne croit encore que la Terre est plate, l’ombre de celle-ci projetée sur la Lune lors des éclipses étant toujours courbe, phénomène qui ne peut s’expliquer que si la Terre est sphérique.

3)   Dit Gersonide ou Ralbag ; né à Bagnols-sur-Cèze en 1288 et décédé à Perpignan le 28 avril 1344.

4)   沈括  ; né à Hangzhou en 1031 et décédé à Zhenjiang en 1095.

5)   梦溪笔谈 ; Meng xi bi tan, écrit en 1088.

6)   De l’arabe المقنطرات, al‑muqanṭarāt, « cercles de la sphère parallèles à l’horizon », dérivé de قنطرة, qanṭara, « arche ».

7)   De l’arabe سمت, (as‑)simt, « le chemin » ; à noter que le mot ne prend pas de « h » final comme en anglais.

8)   Une excellente référence sur les astrolabes, dont le webmestre, James E. Morrison, est malheureusement décédé en avril 2016.

9)   عبدالرحمن الصوفي ; né le 7 décembre 903 à Ray en Perse et décédé le 25 mai 986 à Chiraz en Perse.

Références et suggestions de lecture

• Arabic Way. Planets 1930–2006.
• CHAPMAN, David M.F., éditeur. Observer’s Handbook 2016. Toronto : Royal Astronomical Society of Canada, 2015, ISSN 0080‑4193, ISBN 978‑1‑927879‑05‑4, 352 pages.
• Horizon. (2017‑03‑28). Dans Wikipedia, The Free Encyclopedia. Repéré le 1^er avril 2017 à https://en.wikipedia.org/wiki/Horizon.
• Horizon (physique). (2017‑02‑14). Dans Wikipédia, L’encyclopédie libre. Repéré le 1^er avril 2017 à https://fr.wikipedia.org/wiki/Horizon_(physique).
• KASAK, Enn, et Raul VEEDE. « Understanding Planets in Ancient Mesopotamia. » Folklore Vol. 16, p. 7–33, novembre 2001.
• LITTLE, Robert. Names of the Planets, 2008.
• MEEUS, Jean. Astronomical Algorithms. Deuxième édition. Richmond : Willmann-Bell, 1998, ISBN 0‑943396‑61‑1, 477 pages.
• MORRISON, James E. The Astrolabe. Rehoboth Beach : Janus, 2007, ISBN 978‑0‑939320‑30‑1, 438 pages.
• MORRISON, James E. The Astrolabe. 2016.
• NEUGEBAUER, Otto E. The Exact Sciences in Antiquity. Deuxième édition. New York : Dover, 1969, ISBN 0‑486‑22332‑9, 240 pages.
• PALMIERI, Paolo. « Galileo and the discovery of the phases of Venus. » Journal for the History of Astronomy Vol. 32, Partie 2, N° 107, p. 109–129, mai 2001.
• Pinnule. (2015‑01‑07). Dans Wikipédia, L’encyclopédie libre. Repéré le 21 avril 2017 à https://fr.wikipedia.org/wiki/Pinnule.
• Quora. What is the oldest name for earth?
• Réfraction atmosphérique. (2016‑10‑31). Dans Wikipédia, L’encyclopédie libre. Repéré le 1^er avril 2017 à https://fr.wikipedia.org/wiki/Réfraction_atmosphérique.
• SCHOTTLENDER, Moriel. « Top 10 Ways to Know the Earth is Not Flat. » SmarterThanThat. 19 aout 2008.
• SCHOTTLENDER, Moriel. « 10 Easy Ways You Can Tell For Yourself That The Earth Is Not Flat. » Popular Science. 26 janvier 2016.
• Théorème de Pythagore. (2017‑03‑28). Dans Wikipédia, L’encyclopédie libre. Repéré le 1^er avril 2017 à https://fr.wikipedia.org/wiki/Théorème_de_Pythagore.
• University of Nebraska-Lincoln astronomy education group. Copernican Derivations.
• ZUCKER, Shay. « Hebrew names of the planets. » The Role of Astronomy in Society and Culture, Proceedings of the International Astronomical Union, IAU Symposium Vol. 260, p. 301–305, juin 2011.