Mars a toujours suscité l’imaginaire des humains, de par sa coloration rougeâtre, mais son mouvement apparent dans le ciel de la Terre a donné bien des maux de tête aux astronomes de tous les temps, jusqu’à son solutionnement à la Renaissance. Plutôt que de simuler la position du Soleil dans le ciel, comme nous l’avons fait avec Mercure et Vénus, examinons plutôt comment l’étude astrométrique de Mars a éventuellement permis aux astronomes de déterminer la véritable structure de notre système planétaire.

Premières observations

Samuel Noah Kramer nous a dit que L’Histoire commence à Sumer (en Mésopotamie ; Irak moderne), et c’est le cas aussi pour l’histoire de l’astronomie en général. Ayant plus tard légué sa place aux Amorites, puis aux Akkadiens (séparés en Assyriens au nord et Babyloniens au sud), cette civilisation nous a laissé en héritage la première forme d’écriture, le cunéiforme, de même que plusieurs mythes et légendes, éventuellement repris par les Babyloniens (un groupe akkadien).

C’est des Mésopotamiens que l’on tient la division du zodiaque en douze signes, considérées comme de 30° chacune en astronomie mésopotamienne et, depuis, en astrologie (les constellations zodiacales sont utilisées en astronomie ; leur taille varie, et on en compte treize plutôt que douze, le Soleil traversant la constellation d’Ophiuchus [le Serpentaire], qui est omise dans les signes astrologiques). Même le degré moderne vient d’une unité appelée 𒍑 UŠ, elle-même équivalente à un trentième de 𒆜𒁍 KASKAL.GÍD ou 𒁕𒈾 DA.NA (akkadien bêru), qui représentait deux heures de marche, soit environ 10,75 km ; la circonférence de la Terre était considérée faire 648 000 bêru. De même, la division du degré et celle de l’heure en soixante minutes de soixante secondes sont aussi de reliquats des mathématiques mésopotamiennes, à double base 10 et 60 — par exemple, pour noter le nombre 1 937, on l’aurait décomposé en puissances de 60, soit 32 × 60 + 17, que l’on aurait représenté par 𒌍𒈫𒌋𒐌, soit 30-2-10-7 ; le nombre 763 était représenté par 𒌋𒈫𒐏𒐈, soit 12 × 60 + 43.

Pour les Mésopotamiens, Mars était un avatar du dieu Nergal (𒀭𒄊𒀕𒃲 ^dGIR₃.UNUG.GAL) ; puisque des dieux, on ne peut connaître la pensée, les prêtres-astronomes babyloniens ne cherchèrent pas à comprendre le mouvement de Mars dans le ciel, mais simplement à le suivre. Et c’est ce qu’ils ont fait ! Religieusement (c’est le cas de le dire !), pendant très longtemps, les apparitions et la position de Mars dans le ciel sont strictement notées, de sorte que des cycles de 32, de 47, et de 79 ans sont détectés dans son mouvement. (Il faut aussi noter que Mars n’est présente dans le ciel terrestre que pour une période de quelques mois centrée sur une opposition avec le Soleil se produisant à intervalles d’un peu plus de deux années terrestres.)

Le résultat est que les astronomes mésopotamiens ne savaient pas ce qui « conduisait » Mars, mais pouvaient « prédire » son mouvement en cherchant dans leurs archives pour des apparitions semblables. De plus, les prêtres-astronomes mésopotamiens ne portaient attention qu’à six phénomènes planétaires spécifiques ; c’est maintenant la tradition de les représenter par des lettres grecques :

Tableau . Phénomènes planétaires étudiés par les Mésopotamiens

Planètes inférieures (Mercure, Vénus)		Planètes supérieures (Mars, Jupiter, Saturne)
Ξ	Lever du soir	Γ	Lever héliaque (matin, en même temps que le Soleil)
Ψ	Première station (soir)	Φ	Première station (matin)
Ω	Coucher du soir	Θ	Lever acronyque (au coucher du soleil)
Γ	Lever du matin	Ψ	Deuxième station (soir)
Φ	Seconde station (matin)	Ω	Coucher héliaque (soir)
Σ	Coucher du matin
Source : SWERDLOW, Noel Mark. The Babylonian Theory of the Planets, Princeton, Princeton University Press, 1998, p. 237.

Un premier modèle

Les civilisations mésopotamiennes se font graduellement assimiler par l’Empire perse puis par les Grecs menés par Alexandre le Grand ; dès lors, les livres d’histoire ne parlent presque plus de l’astronomie mésopotamienne, mais plutôt de celle des Grecs.

Il est erroné, toutefois, de penser à ceux-ci comme habitant la seule Grèce moderne, puisque presque toute la côte des mers Égée, Adriatique, Ionienne, et Noire ainsi qu’une bonne partie du littoral méditerranéen du nord sont alors le siège de colonies grecques aussi tôt que vers le septième siècle avant l’ère commune : ainsi, l’un des premiers philosophes grecs, Thalès (Θαλῆς Thalēs ; v. 624/623 – v. 548/545 AÈC), est originaire de Milet, et Turquie moderne.

Plus tard, comme le monde grec entre en contact avec l’Égypte ou l’Empire achéménide, qui succède notamment à l’Empire néo-babylonien et qui en vient à englober l’Égypte pendant un certain temps, culminant avec la conquête des deux derniers par Alexandre le Grand en 332 AÈC, de nombreux échanges se font entre ces trois civilisations. Ainsi, certains philosophes grecs utilisent le calendrier égyptien, principalement pour son uniformité facilitant beaucoup les calculs. Celui-ci est divisé en douze mois de trente jours chacun, plus cinq jours dits épagomènes à la fin de l’année. Puisque la révolution de la Terre autour du Soleil ne dure pas exactement 365 jours, ce calendrier dérive lentement par rapport aux saisons. (Ce calendrier est encore utilisé par l’Église chrétienne copte d’Alexandrie, à la différence près que le calendrier copte a six jours épagomènes plutôt que cinq une fois par quatre ans.)

Tableau . Calendrier égyptien (noms hellénisés)

#	Mois	#	Mois
1	Θωθ Thōth	7	Φαμενώθ Phamenṓth
2	Φαωφί Phaōphí	8	Φαρμουθί Pharmouthí
3	Ἀθύρ Athúr	9	Παχών Pakhṓn
4	Χοιάκ Khoiák	10	Παϋνί Paüní
5	Τυβί Tubí	11	Ἐπιφί Epiphí
6	Μεχίρ Mekhír	12	Μεσορή Mesorḗ
		Jours épagomènes (ἐπαγόμεναι epagómenai)
Source : Egyptian calendar sur Wikipedia, version du 29 janvier 2020 à 20 h 44 min 06.

Pour les philosophes grecs, les planètes n’étaient pas des divinités comme tel, mais plutôt leur emblême — Mars est associé au dieu Πυροεις Pyroëis, mais est appelé Αστηρ Αρειος Astêr Areios, l’étoile d’Arès, un autre dieu. Il devenait donc possible d’imaginer une structure les soutenant et les animant. Puisque la Terre représentait pour eux la moins noble des choses, elle devait être au centre de tout, et les dieux et leurs planètes devaient être de nature différente et circuler autour d’elle. Aussi, puisque le cercle était aux yeux des Grecs la forme la plus parfaite qu’il soit, le mouvement des planètes ne pouvait prendre aucune autre forme et devait être circulaire — et de vitesse uniforme.

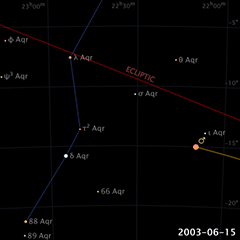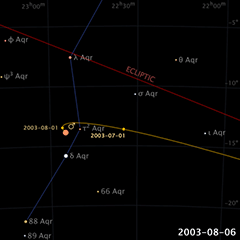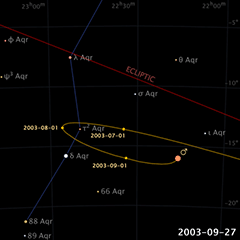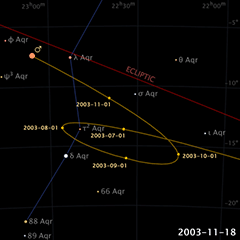Mais un mouvement circulaire uniforme d’ouest en est ne peut expliquer le mouvement rétrograde de Mars — ou de n’importe quelle autre planète — tel qu’illustré dans l’animation (© Eugene Alvin Villar, 2008). L’explication a défié les astronomes pendant longtemps, surtout après que Platon (Πλάτων Plátōn ; 428/427 ou 424/423 – 348/347 AÈC) leur ait donné comme mandat de « préserver les apparences [ou les phénomènes] » (σώζειν τὰ φαινόμενα), tout en s’assurant que ça ne soit qu’avec des cercles et des mouvements uniformes — autrement dit, peu importe la complexité du modèle, pourvu qu’il fonctionne. Le philosophe grec soulignait ainsi l’humilité humaine face aux dieux, desquels notre race ne connaitrait jamais la vraie nature — alors aussi bien user d’imagination ; ça serait toujours inférieur à ce que les dieux eux-mêmes pouvaient faire. En termes modernes, on peut ainsi dire que la plus grande contribution de Platon au domaine de l’astronomie fut de spécifier que celle-ci doit reposer sur des bases scientifiques et mathématiques exactes.

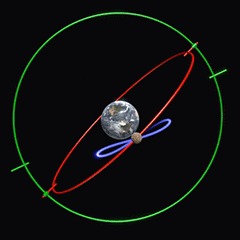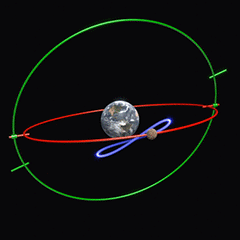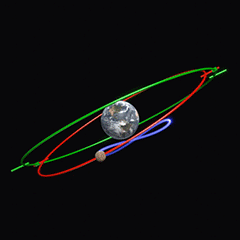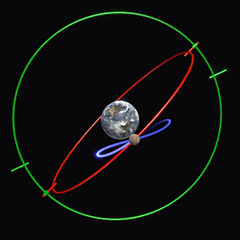Eudoxe de Cnide (Εὔδοξος ὁ Κνίδιος, Eúdoxos ho Knídios ; v. 390 ? – v. 337 AÈC) suggère un système de sphères cristallines centrées sur la Terre. En plus d’une première sphère assurant le mouvement diurne (tour du ciel en 24 heures) et d’une seconde assurant le déplacement graduel de la planète vers l’est d’une nuit à l’autre, il y a deux sphères tournant à la même vitesse l’une que l’autre, mais en directions opposées, la seconde étant accrochée à la première à un certain angle. Il en résulte un mouvement oscillant (appelé hippopède, du grec ἱπποπέδη « entrave de cheval ») qui, selon Eudoxe, explique le mouvement rétrograde (voir animation, créée par The History of Physics).

Le modèle d’Eudoxe explique relativement bien les apparitions planétaires, comme l’indique notre tableau. Selon Evans, « Le seul problème flagrant est la valeur de la période synodique de Mars. Il est à peine possible qu'Eudoxus ait pu commettre une telle erreur, car il suffit de l'observation la plus désinvolte pour réaliser que la période synodique de Mars est supérieure à deux ans. Nous avons donc ici soit un malentendu de la part de Simplicius [des écrits duquel proviennent ces nombres, en référence aux travaux d’Eudoxe], soit une corruption de son texte. » (p. 309).

Tableau . Périodes planétaires selon le modèle d’Eudoxe.

Planète	Modèle d’Eudoxe		Réalité
	PTrop	PSyn	PTrop	PSyn
Mercure	1 an	110 jours	1 an	116 jours
Vénus	1 an	19 mois	1 an	584 jours
Mars	2 ans	8 mois 20 jours	1,88 an	780 jours
Jupiter	12 ans	13 mois	11,86 ans	399 jours
Saturne	30 ans	13 mois	29,42 ans	378 jours
PTrop = Période tropique ; PSyn = Période synodique Source : EVANS, James. The History and Practice of Ancient Astronomy, New York, Oxford University Press, 1998, p. 309.

Malgré l’apparente beauté du modèle d’Eudoxe, celui-ci est bientôt critiqué, notamment par Simplicius, qui indique que les planètes — surtout Vénus et Mars — semblent bien plus près de nous (en jugeant leur éclat apparent) pendant leur boucle de rétrogradation qu’à d’autres moments de leur orbite. Manifestement, si les planètes se déplacent sur des sphères cristallines, leur distance à la Terre demeure fixe, ce qui pose un problème. Selon Simplicius, c’est Autolycos de Pitane (Αὐτόλυκος ὁ Πιταναῖος ; v. 360 – v. 290 AÈC) qui, le premier, mentionne ce changement apparent de distance des planètes, mais on ignore si Autolycos avait tenté de l’expliquer.

Épicycle et déférent

Apollonios de Perga (Ἀπολλώνιος ὁ Περγαῖος Apollốnios o Pergaíos ; v. 240 ? – v. 180 ? AÈC) apporte une piste de solution : selon lui, chaque planète se meut sur un petit cercle, l’épicycle, qui se meut lui-même sur un plus grand cercle, le déférent, que l’on pourrait identifier à l’orbite supposée jusque là. En ajustant les valeurs numériques associées à ce modèle, Apollonios et ses disciples peuvent le faire correspondre beaucoup mieux aux observations que celui d’Eudoxe. Ces paramètres sont les suivants :

• Vitesse angulaire (f_λ) du centre de l’épicycle sur le déférent, soit le taux de changement de la longitude λ̅ ;
• Vitesse angulaire (f_μ) de la planète sur son épicycle, soit le taux de changement de l’anomalie épicyclique μ̄ ;
• Longitude de l’apogée sur le déférent (A) ;
• Valeur initiale de λ̅ pour la date d’origine (λ̅₀) ;
• Valeur initiale de μ̄ pour la date d’origine (μ̄₀) ; et
• Rayon de l’épicycle (r).

Il est plus facile de comprendre l’influence de ces paramètres en consultant l’animation ci-dessous et en modifiant ses paramètres grâce aux glissières de contrôle. (L’animation ne mentionne pas la longitude de l’apogée, qui dépend de la date d’origine des mesures [époque]. Les paramètres de base de l’animation permettent de simuler l’opposition de Mars du 13 octobre 2020 à essentiellement la bonne longitude ; la différence tient principalement au fait que les curseurs de réglage ne permettent pas d’atteindre la précision voulue.)

Le problème que l’on note si on laisse aller l’animation pendant suffisamment longtemps est que les boucles rétrogrades sont toutes de la même taille et espacées du même angle, ce qui n’est pas le cas en réalité — un problème appelé inégalité zodiacale et émanant du fait que les planètes semblent se déplacer plus rapidement dans certaines parties du zodiaque qu’en d’autres. Evans est d’avis que le modèle d’Apollonios était plus une démonstration de principe qu’un modèle mathématique strict ; il évoque d’ailleurs la possibilité que l’astronomie grecque fusse alors de nature qualitative, avant de devenir ultérieurement prédictive et quantitative.

Au centre, mais pas au centre…

Possiblement influencé par l’astronomie babylonienne, Hipparque (Ἵππαρχος, Hipparkhos ; v. 190 – v. 120 AÈC) nota que les divers modèles formulés par les astronomes grecs ne semblaient s’attaquer qu’à un problème à la fois : soit ils expliquaient l’inégalité de la vitesse angulaire dans le temps, soit ils expliquaient les boucles de rétrogradation, mais jamais les deux en même temps — ce qui aurait présumément permis d’expliquer la taille et l’écart variables de celles-ci.

Hipparque venait de présenter un nouveau modèle dans lequel l’orbite apparente (déférent) du Soleil n’est pas centrée par rapport à la Terre, mais légèrement décalée. Ce modèle concordant remarquablement bien avec les observations, Hipparque n’a donc pas hésité à le suggérer pour les planètes. L’écart entre le centre du déférent et la Terre est un nouveau paramètre, appelé excentricité (e) ; on le note ici en terme de fraction du diamètre du déférent.

Comme le montre l’animation ci-dessous, le modèle d’Hipparque peut produire (du moins, avec les paramètres de base, ici valides pour Mars) des boucles de rétrogradation espacées différemment les unes des autres (telles que vues de la Terre), comme il se produit en réalité. (Une liste des oppositions [centres des boucles de rétrogradation] avec leur longitude écliptique s’affichera sous l’animation après que celle-ci soit lancée.)

Malheureusement pour Hipparque, son modèle ne peut pas expliquer à la fois la taille apparente réelle des boucles de rétrogradation ainsi que leur écart apparent réel. C’était néanmoins un pas dans la bonne direction — et Hipparque est passé à l’histoire pour d’autres raisons.

Vitesse égale, mais pas égale

Nous mentionnons plus haut qu’« il est erroné […] de penser [aux philosophes Grecs] comme habitant la seule Grèce moderne », et notre prochain personnage en est un parfait exemple. Claude Ptolémée (Κλαύδιος Πτολεμαῖος Klaúdios Ptolemaîos ; v. 100 ÈC – v. 170 ÈC) est né et a vécu presque toute sa vie en Égypte moderne, mais c’était alors une province de l’Empire romain, mais il écrivait… en grec ! D’ailleurs, « Claude » est un nomen (« nom de famille ») romain, et « Ptolémée » est un nom grec de forme homérique ; plusieurs personnalités grecques l’ont porté.

Si on connaît Ptolémée aujourd’hui, c’est principalement grâce à son œuvre majeure, la Composition mathématique (Μαθηματικὴ Σύνταξις Mathēmatikē Syntaxis), dont les treize livres constituent « la somme des connaissances les plus avancées de l'Antiquité en mathématiques et en astronomie » (Wikipédia). Dans ses éditions ultérieures, l’ouvrage change éventuellement de titre pour La grande Composition, (Ἡ Μεγάλη Σύνταξις Hē Megalē Syntaxis) puis simplement La très grande (Ἡ μεγίστη Hē megiste), arabisé en al-majisṭī (المجسطي), d’où le nom moderne d’Almageste.

Ptolémée a toutefois mis la touche finale à un modèle du système solaire qui allait durer plus de 1 500 ans, malgré de nombreuses critiques, sur lesquelles nous reviendrons. Son « éclair de génie » consiste à avoir ajouté un point imaginaire, l’équant, au-delà du centre du déférent par rapport à la Terre, et depuis lequel la vitesse angulaire de l’épicycle (autrement dit, la longitude moyenne) sur le déférent est uniforme. On ignore au juste comment Ptolémée est arrivé à cette découverte, mais l’astronome grec a peut-être laissé un indice :

[…] ἑκάστου τούτων κατὰ τὸ ὁλοσχερέστερον τῆς ἐπιβολῆς τῆς συνισταμένης ἐκκεντρότητος ἐκ τῆς πελικότητος τῶν περὶ τὰς μεγίστας καὶ ἐλαχίστας ἀποστάσεις τοῦ ἐπικύκλου προηγήσεςν ἡ διὰ τοῦ μεγίστου διαφόρου τῆς παρὰ τὸω ζῳδιακὸν ἀνωμαλίας εὑπισκομένη διπλασίων ἔγγιστα καταλαμβάνεται τὰς δὲ ἀποδείξεις, δι᾽

Sources : HEIBERG, Johan Ludvig. Claudii Ptolemaei Opera Quae Exstant Omnia Volumen I. Syntaxis Mathematica, Pars II, Libros VII–XIII Continens, Leipzig, 1903, p. 317
La version française est traduite à partir de la version anglaise de TOOMER, Gerald James. Ptolemy’s Almagest, Londres, Duckworth, 1984, p. 480 (Book X, Section 6).

En clair, cela signifie que Ptolémée a réalisé « qu’il pouvait préserver l’espacement approprié en laissant le centre du mouvement uniforme à la distance requise de la Terre et tout de même obtenir de bonnes rétrogradations en plaçant le centre du déférent à la moitié de la distance » (Evans, p. 358).

Le modèle de Ptolémée représente un certain affront par rapport à la doctrine prescrite par Aristote (Ἀριστοτέλης Aristotélēs ; 384–322 AÈC) un demi-millénaire plus tôt, à savoir « qu’il n’y a qu’un seul et unique ciel, qu’il est incréé, éternel, et de plus qu’il se meut d’une façon régulière et uniforme » — sous-entendant tout ce qui est contenu dans le ciel de même. Le modèle de Ptolémée propose en effet que les astres changent physiquement de vitesse selon l’endroit où ils se trouvent sur leur orbite. L’astronome grec n’était pas le premier à proposer cela, puisque les Babyloniens utilisaient déjà un système dans lequel la vitesse des planètes est variable selon la portion du ciel où elles se trouvent, mais aucun Grec n’avait jusque là osé aller à l’encontre des enseignements d’Aristote. L’excuse de Ptolémée, si l’on peut dire, est que le mouvement était encore uniforme tel que vu de l’équant ; on verra que cela ne fera pas l’affaire de tous…

Mais la théorie planétaire de Ptolémée avait au moins le mérite d’expliquer convenablement tous les faits observés, soit la rétrogradation des planètes, incluant la largeur des boucles et l’écart entre celles-ci. De plus, gage de la méticulosité de Ptolémée et comme en témoigne le tableau suivant, les valeurs qu’il a déterminées pour l’excentricité, la longitude de l’apogée, et le rayon de l’épicycle de Mars, Jupiter, et Saturne diffèrent très peu des valeurs réelles qu’elles auraient si son modèle était véridique.

Tableau . Éléments des planètes supérieures selon le modèle de Ptolémée.

Valeur	Mars		Jupiter		Saturne
	Ptolémée	Moderne	Ptolémée	Moderne	Ptolémée	Moderne
Excentricité totale	0,200	0,186	0,092	0,096	0,114	0,112
Longitude de l’apogée	115,5°	121°	161°	164°	233°	239°
Rayon de l’épicycle	0,658	0,656	0,192	0,192	0,108	0,105
NOTE : Il s’agit ici des valeurs qu’auraient ces paramètres si le système de Ptolémée était vrai, et non des valeurs réelles de ces paramètres.
Source : PANNEKOEK, Antonie. « The Planetary Theory of Ptolemy. » Popular Astronomy, Vol. LV, No. 9 (1947) : 459–476.

Voici notre animation du modèle de Ptolémée. La différence de vitesse angulaire apparente depuis la Terre n’est pas évidente à remarquer, sauf à forte excentricité ; nous avons donc ajouté un indicateur de celle-ci. Un élément que nous n’illustrons pas ici est que la ligne joignant le centre de l’épicycle à la planète est toujours parallèle à la ligne Terre–Soleil.

(À noter que cette simulation ne produit pas les mêmes oppositions que la simulation du modèle d’Hipparque, puisque nous n’avons pas ajusté les paramètres pour cela, et que la précision des curseurs de contrôle ne permet pas de reproduire toutes les oppositions à l’identique de toute façon. À TITRE DE CURIOSITÉ : Observez l’étrange mais superbe manège de la planète si vous entrez les paramètres suivants : fλ = 0,52°/j ; fμ = -1,26°/j ; r = 0,66 ; e = 0,45 ; et A = 250,00°, puis lancez l’animation.)

À défaut de mieux…

Le modèle de Ptolémée a continué d’être utilisé par les astronomes pendant environ 1 500 ans — malgré les différences entre les observations et les prédictions. Plusieurs facteurs expliquent cette pérennité, notamment des facteurs historiques complètement indépendants de l’astronomie. Comme nous l’avons vu, Ptolémée était un citoyen de l’Empire romain, et celui-ci connut sa fin seulement quelques centaines d’années plus tard — sensiblement le même temps qu’écoulé entre Hipparque et Ptolémée. L’Égypte devint une partie de l’Empire romain d’Orient (plus tard appelé par les historiens « Empire byzantin »), mais celui-ci se distança graduellement de son « frère » d’Occident.

Une bonne partie des volumen (« livres » de papyrus), consignant presque tout le savoir du monde méditerranéen, se trouvait à la Librairie d’Alexandrie, qui fut détruite une centaine d’années après Ptolémée, après être graduellement tombée en désuétude sous la domination romaine de l’Égypte, faute de fonds et de soutien. L’une des rares philosophes restantes, Hypatie (Ὑπατία Hypatía ; v. 355/370 – 415 ÈC, fille de Théon d’Alexandrie [Θέων ὁ Ἀλεξανδρεύς ; v. 335 – v. 405 ÈC]) est assassinée par des chrétiens, cette religion devenant de plus en plus populaire en Égypte ; dès lors, les philosophes ne sont plus vus comme intouchables, et Cyrille d’Alexandrie (Κύριλλος Ἀλεξανδρείας ; Ⲡⲁⲡⲁ Ⲕⲩⲣⲓⲗⲗⲟⲩ ⲁ̅ ou ⲡⲓ̀ⲁⲅⲓⲟⲥ Ⲕⲓⲣⲓⲗⲗⲟⲥ en copte ; v. 376 – 444 ÈC), qui est sans doute à l’origine de ce fait davantage politique que religieux et est pape ou patriarche d’Alexandrie depuis 412, gagne en popularité, ce qui nuit à l’essor de la philosophie, que les chrétiens voient souvent comme contraire à certaines écritures sacrées.

L’Égypte devient une province de l’Empire perse (Sassanide) en 619, puis du Califat rachidun (الخلافة الراشدة al‑ḵilāfa ar‑rāšida) en 646 ; dès lors, elle demeure dans le monde musulman, duquel les chrétiens d’Europe se tiennent relativement loin. Toutefois, les musulmans s’intéressent beaucoup à l’astronomie, et la Grande composition de Ptolémée est recopiée un grand nombre de fois, assurant sa diffusion — et sa survie jusqu’à nous —, les premières traductions en arabe ayant été faites au neuvième siècle. C’est d’une copie arabe que Gérard de Crémone (Gerardus Cremonensis ; v. 1114 – 1187) fait une traduction en latin qui connaît une grande diffusion — bien qu’Henri Aristippe (Henricus Aristippus ; 1105/10 – 1162) ait fait une traduction à partir d’un original grec qu’il a obtenu à Constantinople (Κωνσταντινούπολις Kōnstantinoúpolis ; auj. İstanbul, Turquie) vers 1159 de l’empereur Manuel I^er Comnène (Μανουήλ Α' Κομνηνός Manouếl I Komnênós ; 1118‑11‑28 – 1180‑09‑24), celle-ci n’a pas autant d’impact que la traduction de Gérard. (Certaines sources indiquent plutôt qu’il s’agit d’un élève de l’École de médecine de Salerne qui aurait fait la traduction après avoir trouvé Aristippe observant une éruption sur le mont Etna.)

Pendant tout ce temps, l’Almageste fut retranscrit, traduit, circulé, etc., mais il ne faut pas croire qu’il ait conservé une réputation de marbre. Divers astronomes musulmans ont noté que le modèle de Ptolémée n’était pas parfait dans ses prédictions, ou ont critiqué le fait que le philosophe grec n’ait pas respecté la pensée d’Aristote en donnant des vitesses irrégulières aux planètes. En voici quelques-uns, avec des notes sur leur point de vue.

Tableau . Critiques de Ptolémée dans le monde arabomusulman ou juif.

Nom francisé	Nom arabe ou autre	Biographie	Point de vue
Alhazen	Abū ʿAlī al-Ḥasan ibn al-Ḥasan ibn al-Haytham (أبو علي، الحسن بن الحسن بن الهيثم)	v. 965 Basra (Irak moderne) – v. 1040 Le Caire, Égypte	Auteur des Doutes concernant Ptolémée (شكوك على بطليموس Al‑Shukūkʿalā Baṭlamyūs) et de la Résolution des doutes concernant l’Almageste (تحليل شكوك حول الجست). Le système de Ptolémée ne peut pas exister physiquement, selon lui, et il cherche à solutionner ce problème. Il crée pour ce faire un système géocentrique, mais avec des épicycles additionnels.
Avicenne	Abū ʿAlī al-Ḥusayn ibn ʿAbdillāh ibn al-Ḥasan ibn ʿAlī ibn Sīnā (أبو علي الحسين بن عبد الله بن الحسن بن علي بن سينا)	980 Afshona, Iran moderne – 1037, Hamadān, Iran moderne	Ayant étudié l’Almageste depuis un âge relativement jeune, il en connaît toutes les parties. Il est d’accord avec Ptolémée que la sphère de Vénus doit être avant celle du Soleil, parce qu’il croit avoir observé cette planète passer devant notre étoile (ce qui n’est pas impossible ; il y a eu un tel rare passage de Vénus devant le Soleil le 24 mai 1032, mais Avicenne n’a pas mentionné la date de son observation). Toutefois, il note un mouvement de l’apogée du Soleil, que Ptolémée croyait fixe. (Pour la petite histoire, le crâne d’Avicenne a été retrouvé par les archéologues.)
Averroès	Abū l-Walīd Muḥammad Ibn ʾAḥmad Ibn Rušd (أبو الوليد محمد ابن احمد ابن رشد)	1126 Cordoue – 11 décembre 1198 Marrakech	Réfute les excentriques, épicycles, et déférents. Selon lui, tout mouvement planétaire est circulaire et uniforme, mais il admet vers la fin de sa vie qu’il n’a pas eu tout le temps ou les connaissances nécessaires pour réconcilier ceux-ci avec la pensée d’Aristote. On peut mieux comprendre son raisonnement quand on sait qu’il n’a pas eu accès aux écrits et enseignements d’Eudoxe ou de Callippe de Cyzique, qui avait modifié le système du premier ; les connaître aurait permis à Averroès de comprendre le contexte ayant mené au développement de la théorie planétaire de Ptolémée. À son crédit, on peut lui donner le fait qu’il a mené des observations prouvant la sphéricité de la Terre, et qu’il a plaidé en faveur de la pratique de la philosophie, que d’aucuns voyaient comme contraire à l’Islam ; Averroès la voyait comme permissible et même obligatoire pour une certaine élite.
Moïse Maïmonide ou Maimonides	Rabbi Moshe ben Maimon (רבי משה בן מימון), acronyme « Rambam » (רמב״ם) Abū ʿImrān Mūsā bin Maimūn bin ʿUbaidallāh al-Qurtabī (ابو عمران موسى بن ميمون بن عبيد الله القرطبي) ou Mūsā bin Maymūn (موسى بن ميمون)	1135 ou 1138 Cordoue – 1204 Fostat (Égypte moderne)	Comme Averroès, il croit que les modèles de Ptolémée et même d’Hipparque ne suivent pas les enseignements d’Aristote. De plus, à l’instar des Babyloniens longtemps avant lui, il considère que le mouvement des planètes relève, du moins en partie, du divin et que les humains ne peuvent l’expliquer (ou pas entièrement) par les seules mathématiques.

À noter qu’il serait faux de penser que l’astronomie du Moyen Âge était le seul apanage du monde arabomusulman ; en Europe, toutefois, la pensée astronomique se tournait davantage vers le computus, c’est-à-dire le calcul de la date de Pâques. La pratique était controversée depuis longtemps — dès l’an 154, une rencontre entre le pape Anicet et Polycarpe, évèque de Smyrne, porte notamment sur la différente façon de leur église respective de calculer la date de Pâques, le premier adhérant à l’idéologie occidentale que la fête a lieu le premier dimanche suivant la première pleine lune suivant l’équinoxe de mars, tandis que Polycarpe et son église fêtaient la résurrection du Christ le 14^e jour du mois lunaire (juif) de nissan, en même temps que la Pâque juive (Pessa’h פֶּסַח, latin Pascha).

Le système Terre–Lune à l’échelle. Source : Utilisateur Melikamp sur Wikimedia Commons.

L’orbite de la Lune est toutefois très complexe, notre satellite subissant l’influence gravitationnelle non seulement de la Terre et du Soleil (plus de deux fois l’influence de la Terre), mais aussi celle des autres planètes, principalement Jupiter et Saturne. D’une façon ou d’une autre, elle est difficile à calculer, et Ptolémée dut avoir recours à ce qu’il appela une « seconde anomalie » (aujourd’hui appelée évection) pour tenter de la décrire.

Une révolution tranquille

Le premier clou dans le cercueil de la théorie planétaire de Ptolémée est réellement planté par Mikołaj Kopernik (francisé en Copernic — et son nom, polonais, se prononce [mʲiˈkɔwaj kɔˈpɛrɲik] ; 1473‑02‑19 Toruń, Prusse royale, Royaume de Pologne [Pologne moderne] – 1543‑05‑24 Frombork, principauté-épiscopale de Varmie, Prusse royale, Royaume de Pologne), dans un monumental livre intitulé De revolutionibus orbium cœleſtium (« Des révolutions des orbes célestes »), dans lequel il propose un nouveau modèle du système solaire. Contrairement à presque tous les astronomes avant lui — mentionnons notamment Aristarque de Samos (Ἀρίσταρχος ὁ Σάμιος Aristarkhos ho Samios ; v. 310 – v. 230 AÈC) dans l’Antiquité —, Copernic rend le Soleil fixe près du centre d’un point autour duquel tournent les planètes, incluant la Terre mais à l’exception de la Lune, qui tourne autour de la Terre. Il est à noter que le système de Copernic n’est pas héliocentrique, puisque le Soleil n’en est pas exactement au centre, mais plutôt héliostatique, c’est-à-dire que le Soleil ne bouge pas.

L’œuvre de Copernic est aujourd’hui célébrée, mais il n’y a pas vraiment de « révolution » copernicienne dont on parle souvent aujourd’hui. De revolutonibus est assez froidement accueilli, et le système proposé par Copernic ne fait que déplacer le problème. Wikipédia indique que « pour les planètes extérieures comme Mars, Copernic utilise un point fictif voisin du soleil comme centre d’un cercle sur lequel tourne à vitesse uniforme le centre d’un petit épicycle portant la planète ». Puisqu’il utilise encore des trajectoires exclusivement circulaires, il doit avoir recours aux épicycles et déférents malgré tout — selon son Commentariolus, manuscrit donné à quelques proches avant l’édition de De revolutionibus, ce sont 4 pour la Lune, 3 pour la Terre, 7 pour Mercure, et 5 pour chaque autre planète, pour un total de 34 (une autre source mentionne 48 ; Ptolémée en avait 40, selon cette même source). En termes de complexité, son système n’est pas mieux que celui de Ptolémée — mais on ne juge pas un système à sa simplicité ; cela condamnerait bien le modèle présent, qui, pour tenir compte de l’influence gravitationnelle de tous les corps majeurs du système solaire, a plusieurs milliers de termes mathématiques dans chaque formule ! Mathématiquement, le système de Copernic est équivalent à celui de Ptolémée, à cause du parallélisme précédemment mentionné entre la ligne allant du centre de l’épicycle à la planète et la ligne Terre–Soleil. (Voyez notre animation illustrant la différence entre les positions planétaires observées et celles qu’elles auraient si les orbites étaient toutes circulaires et centrées sur le Soleil, sans déférents ni épicycles.)

Calculer la position d’une planète sur son orbite dans le système de Copernic relève presque de la haute voltige. On doit d’abord calculer la position du Soleil, puis on en arrive par divers calculs à déterminer l’apogée de l’orbite de la planète ainsi que sa « parallaxe » (terme utilisé dans De revolutionibus), pour ensuite chercher ces deux valeurs dans un tableau duquel on extrait des paramètres à additionner ou à soustraire (d’où leur nom d’« additosubstractions ») l’un de l’autre à quelques reprises… pour ensuite soustraire ou ajouter la position du Soleil, et on obtient enfin (!) la position de la planète dans le ciel. Un processus tellement complexe que nous n’avons pas (encore) pu le modéliser par une animation sur cette page.

L’héliogéocentrisme de Tycho

Vivant tout juste après Copernic, mais au royaume de Danemark–Norvège, Tycho Brahe (né Tyge Ottesen Brahe, prononcé [tˢyːə ɒtəsn̩ ˈpʁaːa] ; 1546‑12‑14 château de Knutstorp, Scanie – 1601‑10‑24) en vient rapidement à être reconnu pour la qualité de ses observations astronomiques. Il cerne pratiquement toutes les sources d’erreur possible lors de la prise d’une mesure : position de l’œil de l’observateur, jeu dans les composantes mécaniques de l’instrument, etc. Issu de riches familles danoises (son père, ses deux grands-pères, et tous ses arrières-grands-pères sont membres du Conseil privé du roi), il obtient du roi Frédéric II l’île de Ven (Hven en danois) dans l’Øresund près de Copenhague, dont il devint seigneur féodal. Grâce aux fonds versés par le roi et à ceux recueillis de la cinquantaine de familles vivant sur l’île et maintenant asservies, Tycho construit de 1576 à 1580 un palais-observatoire qu’il appelle Uraniborg (« le Palais d’Uranie », Muse de l’astronomie) et, cinq ans plus tard (1581–1584), un second observatoire appelé Stjerneborg (« palais des Étoiles ») — celui-ci avait la particularité d’être enterré, seuls les toits des différentes pièces dépassant du sol et pouvant être ouverts ou même démontés.

De ses deux observatoires et avec ses instruments qui sont les plus précis et souvent les plus grands jamais vus en Europe, Tycho et ses assistants procèdent à un très grand nombre d’observations astronomiques soigneusement consignées, puis corrigées pour tenir compte des erreurs inhérentes aux instruments et à leurs utilisateurs, et enfin traitées pour en extraire les informations recherchées. Parmi ses découvertes, on note le fait que les comètes sont des astres extérieurs et non des manifestations atmosphériques, et surtout la confirmation que le ciel change, contrairement à ce que l’on pensait dans l’Antiquité, Tycho ayant observé une nova — l’apparition d’une « nouvelle étoile » — en 1572 (on sait aujourd’hui que c’était une supernova, c’est-à-dire l’explosion d’une étoile à la fin de sa vie).

Tycho entend évidemment parler du système proposé par Copernic, mais n’est pas d’accord avec. Selon lui, les planètes tournent autour du Soleil, oui, mais celui-ci tourne autour de la Terre, celle-ci étant à son avis trop massive pour être en mouvement continu ; les astres, quant à eux, sont faits de la « quintessence » mentionnée par Aristote, et ne sont donc pas soumis aux lois de la nature prévalant sur la Terre. Avant lui, Héraclide du Pont (Ἡρακλείδης ὁ Ποντικός Herakleides o Pontikós ; v. 390 – v. 310 AÈC) et Keļallur Nilakantha Somayaji (malayalam : നീലകണ്ഠ സോമയാജി Nīlakaṇṭa Sōmayāji, sanskrit : नीलकण्ठ सोमयाजि ; 1444‑06‑14 – 1544) avaient pensé de même (Héraclide ne considérant toutefois que Mercure et Vénus comme tournant autour du Soleil), à la différence près que ces deux astronomes pensaient que la Terre tourne sur elle-même, tandis que ce n’est pas le cas pour Tycho.

Sortir des sentiers battus

Celui qui ose enfin sortir des sentiers battus — je préfère l’expression anglaise think outside the box ; « penser en dehors de la boîte » — et aller à l’encontre des enseignements des philosophes grecs de l’Antiquité est un disciple et assistant de Tycho, Johannes Kepler (1571‑12‑27 Cité impériale libre de Weil der Stadt, Saint-Empire romain – November 15, 1630‑11‑15, Cité impériale libre de Ratisbonne [Regensburg], Saint-Empire romain — les deux villes se situent en Allemagne moderne). Ayant travaillé pour Tycho, d’abord comme invité puis comme assistant, de 1600 à la mort de ce dernier en octobre 1601, Kepler avait saisi l’importance capitale qu’avaient les observations menées à Uraniborg et Stjerneborg pour l’astrométrie. Malgré les percées accomplies par Copernic et Tycho lui-même pour déterminer une façon de calculer exactement les positions planétaires passées, présentes, et futures, le mouvement de celles-ci échappait encore à la prédiction parfaite, surtout dans le cas de Mars. Tycho avait donc chargé Kepler de déterminer les paramètres de calcul de l’orbite de cette planète, tâche qu’il avait prévue durer deux ans — principalement parce qu’il n’avait pas obtenu de Tycho l’accès à toutes ses observations de Mars ni le droit de recopier les parties auxquelles il avait accès pour son propre usage — mais qui lui en prendra huit.

Dès le départ, Kepler est d’avis que c’est Copernic et non Tycho qui voit juste dans sa perception du monde : toutes les planètes tournent autour du Soleil, incluant la Terre. Tandis que Copernic n’explique pas pourquoi la Lune tourne plutôt autour de la Terre que du Soleil, ce qu’on lui reproche d’ailleurs, pointant sa théorie comme incomplète, Kepler suppose en 1600 que :

In Terra inest virtus, quae Lunam ciet

Source : CASPAR, Max. Kepler, traduit par Clarisse Doris HELLMAN, New York, Dover / Courier, 1993, ISBN 978‑0‑486‑67605‑0, p. 110,
citant un essai adressé à l’archiduc Frédéric d’Autriche, futur empereur Frédéric II du Saint-Empire, à ne pas confondre avec Frédéric II de Danemark–Norvège précédemment mentionné.

préfigurant ainsi la notion de gravitation universelle sur laquelle nous reviendrons bientôt. Cette perspicacité demeure avec lui et, le 11 octobre 1605, il écrit à David Fabricius (1564‑03‑09 Esens – 1617‑05‑07 Osteel, les deux en Allemagne moderne) que « l’orbite d’une planète est une ellipse », ce qu’il consignera définitivement dans Astronomia Nova (« La nouvelle astronomie ») en 1609, puis dans Harmonices Mundi (« L’harmonie des mondes ») en 1621. Avec un léger complément, cette phrase devient sa première loi :

Jam igitur hoc habeo Fabrici: Viam planetae verissimam esse Ellipsin, quam Durerus itidem oualem dixit, aut certè insensibili aliquo ab Ellipsi differentem.

Source : von DYCK, Walther, et Max CASPAR. Johannes Kepler Gesammelte Werke, Tome XV, Munich, C.H. Beck’sche, 1951, p. 249.

Dans l’édition finale d’Harmonices Mundi, cette loi s’est fait rejoindre par deux autres, qui décrivent encore aujourd’hui le mouvement des planètes :

• L’orbite d’une planète est une ellipse dont le Soleil occupe l’un des foyers ;
• Une ligne joignant une planète au Soleil balaie des aires égales en des temps égaux ; et
• Le carré de la période orbitale d’une planète est directement proportionnel au cube du demi-grand axe de son orbite.

En termes mathématiques, les deuxième et troisième lois peuvent respectivement être exprimées ainsi :

• E_n + 1 = E_n − (E_n − e · sin E_n − M) ÷ (1 − e · cos E_n) ; et
• a³ ⁄ P² = k

La troisième loi de Kepler tient remarquablement bien dans le système solaire, comme en fait foi le tableau suivant :

Tableau . Distance moyenne au Soleil et période de révolution de chaque planète, et proportions de chacune.

Planète	Distance au Soleil (a), en millions de kilomètres	a³	Temps de révolution (P), en jours	P²	a³ ÷ P²
PLANÈTES MAJEURES
Mercure	57,909	194 195,068	87,969	7 738,563	2,509E+1
Vénus	108,208	1 267 004,363	224,701	50 490,539	2,509E+1
Terre	149,598	3 347 937,657	365,256	133 411,946	2,509E+1
Mars	227,939	11 842 841,473	686,971	471 929,155	2,509E+1
Jupiter	778,570	471 946 746,142	4 332,590	18 771 336,108	2,514E+1
Saturne	1 433,530	2 945 915 992,248	10 759,220	115 760 815,008	2,545E+1
Uranus	2 875,040	23 764 663 763,800	30 688,500	941 784 032,250	2,523E+1
Neptune	4 500,000	91 125 000 000,000	60 183,000	3 621 993 489,000	2,516E+1
SATELLITES DE JUPITER (distances en km)
Io	421 700,000	74 991 286 313 000 000,000	1,769	3,130	2,396E+16
Europa	671 034,000	302 157 637 909 067 328,000	3,551	12,611	2,396E+16
Ganymède	1 070 412,000	1 226 458 641 348 174 592,000	7,155	51,188	2,396E+16
Callisto	1 882 709,000	6 673 437 478 841 326 592,000	16,689	278,523	2,396E+16
SATELLITES DE SATURNE (distances en km)
Mimas	185 539,000	6 387 128 220 745 819,000	0,942	0,887	7,198E+15
Enceladus	237 948,000	13 472 437 466 515 392,000	1,370	1,877	7,176E+15
Tethys	294 619,000	25 573 033 837 178 660,000	1,888	3,564	7,176E+15
Dione	377 396,000	53 751 659 672 995 136,000	2,737	7,491	7,176E+15
Rhea	527 108,000	146 453 185 638 043 712,000	4,518	20,414	7,174E+15
Titan	1 221 870,000	1 824 210 729 193 202 944,000	15,945	254,243	7,175E+15
Iapetus	3 560 820,000	45 149 200 237 783 367 680,000	79,322	6 291,900	7,176E+15
La relation est moins précise pour les planètes externes, puisque leur masse plus grande fait en sorte qu’elles ont une influence gravitationnelle plus marquée sur le Soleil et entre elles ; il en va de même pour Mimas, satellite de Saturne, qui est fortement déstabilisé par les autres satellites de Saturne, principalement Titan. À noter que pour un autre corps central que le Soleil, la valeur de a³ ÷ P² est différente.

Il importe de préciser que le modèle de Kepler n’est qu’une approximation — on s’en rendra compte plus tard —, puisque chaque corps du système solaire subit l’influence gravitationnelle de chaque autre, ce qui perturbe toutes les orbites ; à strictement parler, seule l’orbite instantanée d’une planète autour du Soleil (ou d’un satellite autour d’une planète, comme il s’avère par la suite) peut être considérée comme elliptique. Les astronomes utilisent aujourd’hui le terme d’orbite osculatrice pour désigner l’orbite qu’un aurait à un moment précis en l’absence de perturbations. Sept éléments sont requis pour déterminer l’orbite d’un astre et sa position le long de celle-ci :

Tableau . Éléments orbitaux osculateurs d’un astre orbitant autour du Soleil, avec valeurs pour la Terre, Mars, et la comète Encke.

Élément	Description	Valeurs
		Terre	Mars	Encke
Époque	Moment auquel les éléments orbitaux osculateurs sont valides.	J2000.0, soit le 1er janvier 2000 à 12 h 00 TT (jour julien 2451545,0)  Soit à 11 h 58 min 55,816 s UTC (11 h 59 min 27,816 s TAI).		JJ 2457147,5
M₀ ou T ou L	Anomalie moyenne à l’époque, ou jour julien du passage au périhélie ou longitude moyenne à l’époque.	L = 100,466°	L = 355,433°	M = 158,212° T = 2456618,277
a	Demi-grand axe de l’orbite, en unités astronomiques.	1 u.a.	1,523 u.a.	2,215 u.a.
e	Excentricité de l’orbite.	0,017°	0,093°	0,848°
i	Inclinaison de l’orbite par rapport à l’écliptique, en degrés.	0°	1,850°	11,782°
Ω	Longitude du nœud ascendant ; l’angle, mesuré le long de l’écliptique, entre le point de référence (point vernal ♈︎) et l’endroit où l’orbite croise l’écliptique du sud (« dessous ») vers le nord (« dessus »).	174,873°	49,558°	334,568°
ω ou π  Le symbole ϖ (poméga) est parfois utilisé pour désigner la longitude du périhélie, mais il n’est pas recommandé puisqu’il ressemble trop à ω, ce qui pourrait engendrer de la confusion. Il faut aussi éviter de confondre le symbole de la longitude du périhélie avec π = 3,14159265…	Argument du périhélie ; l’angle, mesuré le long de l’orbite, entre le nœud ascendant et le périhélie, ou longitude du périhélie ; la longitude qu’aurait le périhélie par rapport au point vernal si l’inclinaison de l’orbite en question était nulle — cette valeur est égale à la somme de l’argument du périhélie et de la longitude du nœud ascendant  Bien que ces angles sont mesurés sur deux plans différents. .	102,937°	336,060°	186,545°

Et tombe la pomme, et tombe la Lune

On raconte qu’Isaac Newton (1643‑01‑04, Woolsthorpe-by-Colsterworth, Lincolnshire, Angleterre – 1727‑03‑31 Kensington, Middlesex, Angleterre) aurait eu son éclair de génie après avoir reçu une pomme sur la tête. Cette histoire est partiellement fausse ; bien que la chute d’une pomme soit sans doute à l’origine de sa découverte, c’est probablement arrivé à quelques mètres de lui. Mais c’est le résultat qui compte vraiment, et en voyant cela, Newton a supposé que les astres sont sujets à la même force de gravité que nous et les choses qui nous entourent sur Terre. Jusque là, on croyait les astres faits d’une autre matière — la « quintessence » ou le « cinquième élément », voire l’« éther » — de nature divine et non sujette à la gravité. Et si, Newton supposa, la Lune « tombait » vers la Terre, et celle-ci, vers le Soleil, à cause de la gravité ?

Newton avait pu s’affranchir de l’idée de la quintessence suite aux observations lunaires de Galilée. Le 30 novembre 1609, cet astronome italien avait pointé sa petite lunette d’approche vers la Lune et remarqué les accidents de relief à sa surface. Galileo Galilei, de son nom complet (1564‑02‑15 Pise, Duché de Florence – 1642‑01‑08 Arcetri, Grand-Duché de Toscagne), fut le premier à déduire que ces différences d’ombres étaient causées par des montagnes, des vallées, et des cratères à la surface de notre satellite. L’Italien était d’avis que l’Univers peut être décrit en termes mathématiques ; cela constituait une autre avenue pour Newton.

Dans son œuvre maîtresse, Philosophiæ Naturalis Principia Mathematica, (dont la copie personnelle, annotée par Newton, de la première édition peut être consultée dans la Bibliothèque en ligne de l’Université de Cambridge), le physicien anglais énonce les trois lois du mouvement qui portent maintenant son nom :

Lex. I.
Corpus omne perſeverare in ſtatu ſuo quieſcendi vel movendi uniformiter in directum, niſi quatenus a viribus impreſſis cogitur ſtatum illum mutare.
[…]
Lex. II.
Mutationem motus proportionalem eſſe vi motrici impreſſæ, & fieri ſecundum lineam rectam qua vis illa imprimitur.
[…]
Lex. III.
Actioni contrariam ſemper & æqualem eſſe reactionem : ſive corporum duorum actiones in ſe mutuo ſemper eſſe æquales & in partes contrarias dirigi.

Sources : NEWTON, Isaac. Philosophiæ Naturalis Principia Mathematica, première édition, Londres, Joseph Straeter, 1687, p. 12–13, pour la version originale latine, et NEWTON, Isaac, traduit par Émilie DU CHÂTELET. Principes mathématiques de la philosophie naturelle, Paris, Alexis Clairaut, 1756, pour la version française, citée par Wikipédia. À noter que Newton a rayé, dans sa copie de la première édition, la première partie (jusqu’à « ſive ») de la troisième loi. Chaque loi est aussi suivie d’un paragraphe d’explication, que nous avons ici omis.

Les trois lois de Kepler précédemment mentionnées découlent des trois lois de Newton ; si ce dernier avait fait sa découverte avant l’Allemand, ce dernier aurait certainement eu une place moindre dans l’Histoire. À l’inverse, toutefois, il est impossible de dériver les lois de Newton à partir de celles de Kepler.

En termes mathématiques, les trois lois peuvent s’énoncer ainsi :

• ∑F = 0 ⇔ dv ⁄ dt = 0
• F = dp ⁄ dt = d(mv) ⁄ dt = m(dv ⁄ dt) = ma
• F_A = −F_B

La première loi de Newton est une reformulation de la loi de l’inertie, qui avait été originalement formulée par Galilée, à qui Newton a donné le crédit approprié. D’ailleurs, l’Anglais a un jour écrit à Robert Hooke : « Si j'ai vu plus loin, c'est en montant sur les épaules de géants. »

Newton est aussi à l’origine de la théorie de la gravitation universelle (aussi publiée dans les Principia) : « Deux corps ponctuels de masses respectives M_A et M_B s’attirent avec des forces vectoriellement opposées et de même valeur absolue. Cette valeur est proportionnelle au produit des deux masses, et inversement proportionnelle au carré de la distance qui les sépare. Ces [deux] forces opposées ont pour axe commun la droite passant par les centres de gravité de ces deux corps. » [Source : Wikipédia.] (Elle n’a pas été découverte par Newton, mais c’est lui qui l’a formalisée ainsi.) On la représente habituellement par la formule F_A⁄B = F_B⁄A = G[(M_AM_B) ⁄ d², où G est la constante gravitationnelle, égale à 6,67430(15) × 10⁻¹¹ m³ kg⁻¹ s⁻². Étrangement, c’est l’une des constantes de la nature que l’on connaît le moins bien : cela s’explique notamment par les faits que a) la force de gravité est la plus faible des forces fondamentales de la nature ; et b) il est impossible de se libérer complètement de l’influence d’autres masses que celles étudiées. On connaît mieux le paramètre gravitationnel (héliocentrique) standard, μ = GM = 398 600,4418 ± 0,0008 km³ · s⁻², où M est la masse du Soleil — comme la connaissance de G dépend de celle de M et vice versa, aucune de ces deux valeurs n’est connue avec grande précision.

Avance du périhélie de Mercure

La dernière brique au casse-tête de la détermination précise des orbites planétaires a été apportée il y a une centaine d’années à peine, par un ancien préposé de l’Institut fédéral de la propriété intellectuelle de Berne, en Suisse, mieux connu pour une équation n’ayant rien à voir avec la mécanique céleste, soit la célèbre E = mc².

Le problème se trouvait à l’intérieur de l’orbite de la Terre et à trait à celle de la planète Mercure. En effet, le périhélie (point le plus proche du Soleil) de celle-ci avance de quelque 42″/siècle plus vite que le prédit la théorie de la gravitation universelle de Newton. Il importe ici de préciser que le modèle de Newton prédisait le mouvement du périhélie de Mercure, mais en moindre partie qu’observé : en effet, le mouvement de précession observé est de 574,10 ± 0,65″/siècle, tandis que Newton prédit 532,3035″/siècle ; c’est la différence de 42″/siècle qui n’était pas expliquée.

Selon la Théorie de la Relativité générale d’Einstein, l’espace-temps lui-même est courbe, et l’orbite doit avoir un mouvement de précession. On notera que Mercure n’est pas la seule planète dont le périhélie bouge plus rapidement que prévu par la théorie de Newton, mais, du fait de sa proximité au Soleil, c’est celle pour laquelle l’effet est le plus grand — il n’est que de 3,84″ par siècle pour la Terre, et 8,62″ par siècle pour Vénus…

Théorie planétaire moderne

Nous l’avons vu, le modèle de Kepler ne s’applique strictement que dans le cas où deux objets sont isolés, ce qui n’est jamais le cas dans la nature. Afin d’obtenir des résultats exacts, il faut donc tenir compte de l’influence gravitationnelle des autres planètes ; la tâche, qui n’est pas mince, est de solutionner le « problème à N corps » (anglais « n‑body problem »). Pour ce faire, il faudrait connaître, à un moment précis, la position exacte et la vitesse exacte (en fait, le vecteur de mouvement exact) de chaque corps du système solaire, si petit et peu massif soit-il. En pratique, ceci est impossible, et de toute façon, une solution képlerienne au problème négligerait d’autres forces que celle de la gravité ; or, celles-ci peuvent avoir un effet dans certains cas particuliers.

Aujourd’hui, deux théories planétaires sont couramment utilisées : la théorie semi-analytique VSOP (variations séculaires des orbites planétaires), développée à l’origine par Pierre Bretagnon (1942–2002) et reprise par l’Institut de mécanique céleste et de calcul des éphémérides (IMCCE) (à l’Observatoire de Paris) depuis sa fondation en 1998 ; et la théorie DE (Development Ephemeris) du Jet Propulsion Laboratory de la NASA. Chacune a un référentiel différent, et les résultats obtenus par l’une peuvent différer de ceux obtenus par l’autre à cause de cela — l’IMCCE indique dans la Connaissance des temps pour 2019 que « le repère de référence de VSOP ne correspond pas à celui de DE403. ». De même, chacune a connu diverses versions dans le temps : de la VSOP82 originale établie en 1982, on en est maintenant à VSOP2013 ; la DE a commencé dans les années 1960 et en est maintenant à DE438 (2018). Une version réduite du VSOP87 se trouve dans le livre Astronomical Algorithms de Jean Meeus. Les logiciels modernes utilisent une ou l’autre des versions, parfois en concurrence ou au choix de l’utilisateur.

Astronomie‑Québec utilise dans ses pages web une adaptation JavaScript de VSOP87.

Conclusion

L’astronomie de position a fait d’immenses progrès depuis les Babyloniens. Les modèles numériques modernes que sont VSOP2013 et DE438 permettent de calculer avec précision la position des planètes pour une période de temps de plusieurs dizaines de milliers d’années. Ce progrès a été rendu possible par plusieurs personnages historiques, et repose parfois sur une ouverture d’esprit et un éloignement des paradigmes fixés par d’autres. Si on peut voir si loin aujourd’hui, c’est vraiment parce que l’on a grimpé sur les épaules de géants.

🌑 🌒 🌓 🌔 🌕 🌖 🌗 🌘

© 2020 Astronomie‑Québec / Pierre Paquette